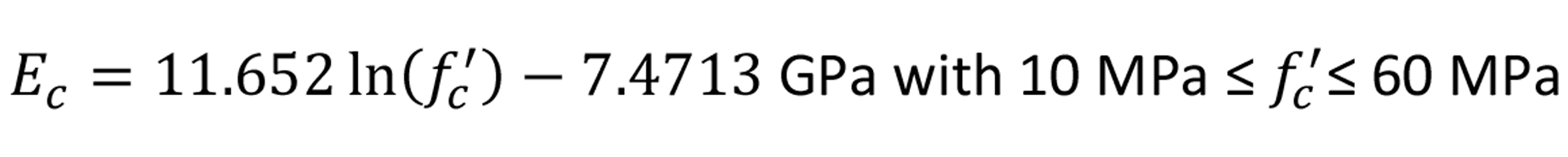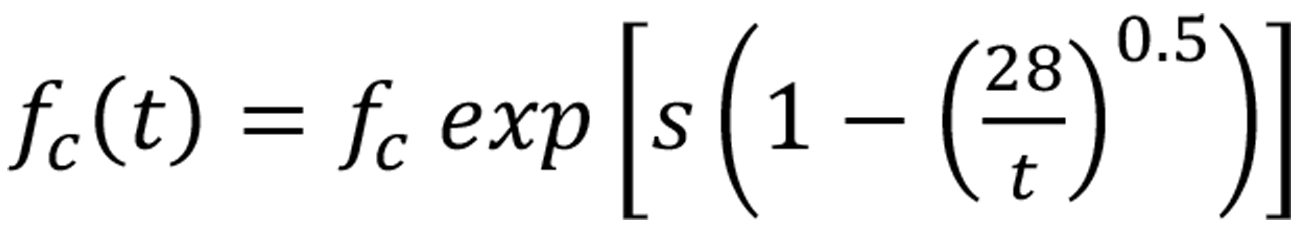Elastic Modulus For Concrete

Dr. N. Subramanian Ph.D., FNAE Gaithersburg, Maryland, USA

 

Concrete is not an elastic material, that is, it will not recover its original shape on unloading. In addition, the stress-strain curve of concrete is non-linear. Hence, modulus of elasticity and Poisson’s ratio, which are elastic constants, are not applicable. However, for the sake of simplicity, they are used in the analysis and design of concrete structures, assuming elastic behavior. The modulus of elasticity of concrete is required for the estimation of the deformation of buildings and members. In addition, it is used for determining the modular ratio,m. High-strength concrete (HSC) will have a higher modulus of elasticity and hence will result in reduced deflection and increased tensile strength.

The modulus of elasticity is dependent on the compressive strength of concrete, properties of the coarse aggregates, the proportion of the aggregates in the concrete, quality of cement paste and addition of mineral admixtures (Zhang and Gjvorv, 1991, Neville, 1996). Modulus of elasticity, however, is affected to a lesser extent by the chemical and mineral admixtures, curing conditions, age of the concrete and the type of cement (Russian Standard SP 52-101:2003). The fine and coarse aggregates generally occupy 60% to 75% of the volume of concrete (70% to 85% by mass) and are stiffer than the concrete paste (Neville, 1996). Hence, their E-value will have a significant effect on the E-value of concrete. The use of dense aggregates such as basalt than limestone, which in turn results in a higher modulus than lightweight aggregates. Specifying the largest practical maximum size of aggregate and a suitable grading may result in higher content of coarse aggregate in a concrete mixture. Such concretes tend to have a higher modulus of elasticity, provided the aggregates used have a high modulus of elasticity (Crouch et al., 2007). However, increasing the coarse aggregate size may result in reduced strength in high-strength concrete mixtures. Increasing the paste content may decrease the void content of concrete, and hence may increase the modulus of elasticity. Increasing the water-cement ratio will reduce the value of modulus of elasticity, similar to its effect on the compressive strength of concrete. A high modulus of elasticity is associated with a higher compressive strength of concrete, although the two are not directly proportional. For example, to increase the modulus of elasticity by 20% it may be necessary to increase the strength by 50%. Aïtcin, 2011 observes that the modulus of elasticity of concrete is as important as the water-cement ratio of the concrete mixture. Fig. 1 shows the various factors that may affect the modulus of elasticity of concrete.

Modulus of elasticity may be determined using an extensometer attached to the compression test specimen as described in IS 516:1959 or ASTM-C469M-14 (Subramanian, 2019). The test set-up for measuring the modulus of elasticity is shown in Fig. 2. 

Fig. 1: Factors Affecting Modulus of Concrete

Accurate prediction of modulus of elasticity is important in reinforced and pre-stressed concrete structures while calculating member deformations, elastic shortening of columns, shrinkage and creep loss as well as crack width. Note that restricting the crack width is directly related to the durability of concrete structures. The modulus of elasticity is also required in seismic analysis for rational calculation of drift and deformations.

Modulus Of Elasticity Of Concrete

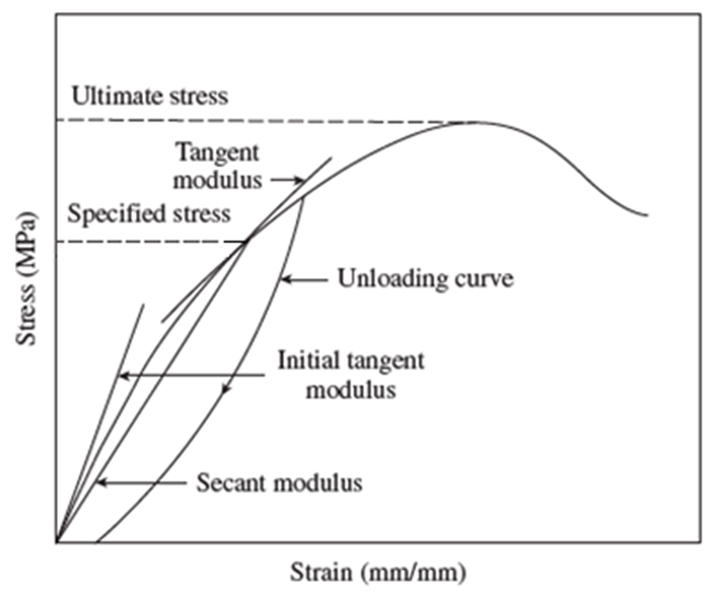
The modulus of elasticity of concrete is defined as the ratio of normal stress to corresponding strain for tensile or compressive stresses below the proportional limit of the material. When the loading is of low intensity and short duration, the initial portion of the stress-strain curve of concrete in compression is linear, justifying the use of modulus of elasticity. When there is sustained load, however, the stress-strain curve will become nonlinear, even at relatively low stresses, due to inelastic creep. Moreover, the effects of creep and shrinkage will make the concrete behave in a non-linear manner. Hence, the initial tangent modulus is considered to be a measure of the dynamic modulus of elasticity (Neville and Brooks 2010). When the linear elastic analysis is used, one should use the static modulus of elasticity. Various definitions of modulus of elasticity are available: initial tangent modulus, tangent modulus (at a specified stress level), and secant modulus (at a specified stress level), as shown in Fig. 3. Among these, the secant modulus, which is the slope of a line drawn from the origin to the point on the stress-strain curve corresponding to 40% of the failure stress, is considered the average value of Ec under service load conditions (Neville and Brooks 2010).

Fig. 2: Test set-up for Measuring the Modulus of Elasticity of Concrete

 

Expressions Suggested By Different Codes

Different national codes suggest different expressions for the determination of the modulus of elasticity of concrete, to be used in the design. These expressions are given below. 

For normal-weight concrete, Clause 19.2.2.1 of ACI 318M-19 code allows it to be taken as

1. 

Where is the cylinder compressive strength of concrete in MPa.

Clause 8.6.2.3 of the Canadian code CSA A23.3-14 gives a similar expression, for normal density concrete with a compressive strength between 20 and 40 MPa as

2. 

Clause 6.2.3.1 of IS 456: 2000 suggests that the short-term static modulus of elasticity of concrete, Ec, may be taken as

3. 

Where is the cube compressive strength of concrete in MPa.

Both IS 456 and ACI 318 caution that the actual measured values may differ by about 20 % from the values obtained from Eq. (1). Moreover, the US code value is 16% less than the value specified by the Indian code. It has to be noted that the use of a lower value of E_c will result in a conservative (higher) estimate of the short-term elastic deflection.

For both normal-strength (NSC) and high-strength (HSC) concrete, the Comité Euro-International du Béton and the Fédération Internationale de la Précontrainte (CEB-FIP) Model Code and Euro code 2 suggest that the approximate value of secant modulus Ecm of concrete with quartzite aggregates can be obtained from the mean compressive strength as below

4. 

Where  =  + 8 MPa, and  is the cylinder compressive strength of concrete The coefficient α present only in the CEB-FIP Model code has a value of 1.2 for basalt and dense limestone, 1.0 for quartzite, 0.9 for limestone, and 0.7 for sandstone aggregates. When lightweight aggregates are used, the CEB-FIP equation was found to overestimates the modulus, and the calculated values decreased when coarse aggregate such as crushed quartzite, crushed limestone, and calcined bauxite was used (Vakhshouri and Nejadi, 2019).

Fig. 3: Various Definitions of Modulus of Elasticity of Concrete

Effect Of Unit Weight Of Concrete On The Modulus Of Elasticity

There is an increased awareness and use of lightweight concrete (LWC) in applications like elevated slab structures; bridge decks; wall, ceiling, and floor insulation; and insulation for fire protection. LWC normally has an in-place density of 800 to 2240 kg/m3. It is traditionally produced using lightweight aggregates such as expanded shale or clay, vermiculite, pumice, or scoria; however, it can be also produced using foaming technologies and polystyrene beads. Only a few codes provide formulae for the modulus of elasticity considering the density of concrete.

Clause 19.2.2.1 of ACI 318:2019 and also the AASHTO-LFRD-2006, provide the following formula for the modulus of elasticity, considering the density (unit weight) of concrete

5. 

where ρ_c is the unit weight of concrete (varies between 1440 kg/m³ and 2560 kg/m³).

As per clause 8.6.2.2 of the Canadian code, the modulus of elasticity, E_c for concrete with ρ_c between 1500 and 2500 kg/m³ may be taken as

6. 

where ρc is the unit weight of concrete.

The Australian code AS 3600:2018, clause 3.1.2 specifies that the modulus of elasticity be taken as below noting that this value may have a range of ± 20%

7. 

Where,  is the mean value of the in-situ compressive strength of concrete at the relevant age.

Table 3.1.2 of AS 3600:2018 gives the values of Ec calculated as per Eqn. (7) and is shown in Table 1.

The Architectural Institute of Japan specifies the following equation to estimate the modulus of elasticity of concrete

8.

As per BS 8110-2, 1985, the elastic modulus is related to its compressive strength as below

9. 

The equation for elastic modulus in the Russian SP 52-101-2003 has a different format as shown below:

10. 

High Strength Concrete

High-strength concrete (HSC) is often used in the columns of high-rise buildings, long-span bridges, parking garages, and offshore structures, where improved density, lower permeability, and increased resistance to freeze-thaw and corrosion are required. In these applications, designers can take full advantage of the increased compressive strength of HSC to reduce the amount of steel, reduce column size (to increase usable floor space in high-rise buildings), or allow additional stories. These benefits overshadow the higher cost of raw materials and increased quality control costs involved with HSC.

The ACI committee report on HSC (ACI 363R-92) provides the following equation for modulus of elasticity, which has also been adopted by NZS 3101- Part 1:2006.

11. 

The results of the above equation and also Eq. (1) of ACI 318-19, with the experimental values of several researchers, are compared in Fig. 4. It is seen that the ACI 318-19 expression overestimates the modulus of elasticity for concretes with compressive strengths over 41 MPa, and the Eqn. (11) provides better correlation, especially for high-strength concrete.

Fig.4: Modulus of Elasticity Versus Concrete Strength

Clause 3.1.2 of the Australian code AS 3600:2018, suggest the following equation, noting that this value may have a range of ± 20%

12. 

The Japanese code JSCE (2007) Clause 4.1.2 [equation C4.1.3] gives the following equation,

13. 

Where Ec(t) is the effective Young’s modulus at the age of t days; ф(t) is the compensating factor taking account of creep during concrete temperature increasing for up to 3 days ф =0.73, for after 5 days ф =1.0 (linear interpolation can be used from 3 to 5 days) and   (t) is the estimated compressive strength of concrete at t days.

The equations given in the various codes are simple to use because they require only the compressive strength and the concrete density to determine the value of the elastic modulus of concrete. Vakhshouri and Nejadi, 2019 have collated and presented the various other empirical models suggested by other researchers to predict the elastic modulus of normal strength concrete.

Swamy, 1985 showed that the elastic modulus for high strength concrete did not increase in proportion to its strength and the maximum value of modulus will be in the range of 45 to 50 GPa only.

Effect of Different Types of Aggregates of the Elastic Modulus

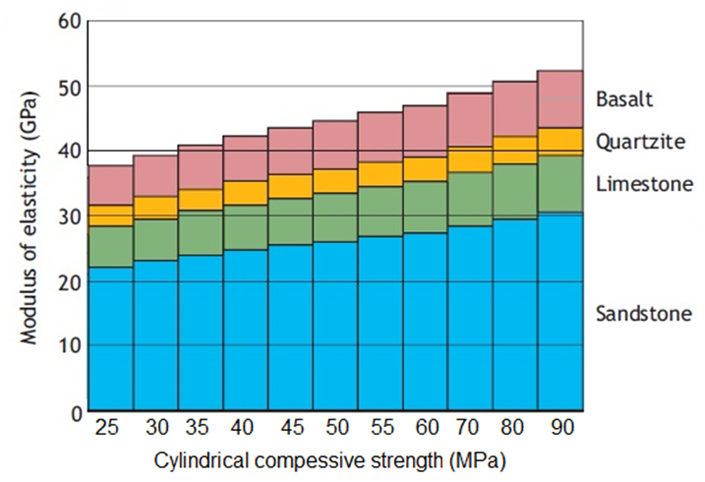
The equations discussed till now may not be accurate for concrete with all types of aggregates. It is because the elastic modulus and the compressive strength are influenced by several other factors, such as the type of aggregate, humidity, age of the concrete, and the type of binder used. As per Eurocode 2, the value of elastic modulus Ecm as computed by using equation (4), should be reduced for concrete with limestone and sandstone aggregates by 10% and 30% respectively. For basalt aggregates, the value should be increased by 20%. Though not mentioned in the Eurocode 2, equation (4) for concrete with quartzite aggregates is also valid for concrete with siliceous aggregates (Bamforth, et al., 2008). The value of the elastic modulus, for various values of cylinder compressive strength  and for different aggregates, as per Eurocode 2, is shown in Fig. 5.

Fig. 5: Modulus of Elasticity of Concrete with Different Aggregates related to the Compressive Strength of Concrete

Only when very high strength concrete is used, the type of aggregate will be known to the designer and hence can be used to predict the value of elastic modulus as per Fig.5. In the case of normal strength concrete, the designer will not know the type of aggregate used, until the concrete supplier is selected. Hence they should exercise caution while using the value of elastic modulus as per Fig.5.

Bamforth, et al., 2008 also recommend testing concrete specimens when the elastic modulus is critical for the performance of any structure. They also suggest adopting the following while designing structures:

• Use the mean value of Ecm for serviceability calculations
• Use a partial safety factor of γcE of 2, to get the design value of elastic modulus, Ecd = Ecm /γcE and use it in ultimate limit state calculations
• Use an effective modulus, Ec,eff =Ecm / (1+ф), where where ф is the creep coefficient, to take care of creep in long-term deflection calculations. The value of the creep coefficient, ф, may range between 1 and 3 (See Bamforth, et , 2008).

Noguchi and Tomosawa, 1995 and Noguchi, et al., 2009 proposed the following equation which applies to a wide range of aggregates and mineral admixtures used in concrete.

14. (a).
    
     

where the correction factors k1 and k2 are given in Tables 2 and 3.

Substituting k1 = 1.0 and k2 = 1.0 and simplifying we get .

14(b). 

Fig. 6 shows the variation of strength and modulus of elasticity of concrete, made with different aggregates, calculated as per Eurocode 2 (Bamforth et al., 2008).

The dashed lines in Fig. 6 represent the values calculated by Bamforth et al., 1997 based on aggregate E-value and concrete strength for concrete used in nuclear Power Station Structures.

Fig. 6: Variation of Strength and Modulus of Elasticity of Concrete with Different Aggregates

A comparison of different formulae for the static elastic modulus of concrete is provided in Fig. 7. From Fig. 7 it is also seen that the values calculated as per Euro code 2 expression (Eqn. 4) provide the upper bound and those calculated using Noguchi, et al. (2009) (Eqn. 14) provide the lower bound values. As Eqn. 14 considers a wide range of aggregates and mineral admixtures used in concrete and also gives lower bound values, it is suggested to be included in the future versions of IS 456, instead of Eqn. 3, which considers only the compressive strength of concrete.

Fig. 7: Comparison of Different Formulae for the Static Elastic Modulus of Concrete

Variation Of Modulus Of Elasticity With Time

The value of modulus of elasticity varies with time (Singh et al., 2013). As per Clause 3.1.3(c) of Euro code 2, this time-dependent value of Ec(t) can be determined using the following expression

15(a).

Where Ec(t) and fc(t) are the modulus of elasticity and mean compressive strength ofconcrete at time t and Ec and fc aretherespective values determined at an age of 28 days. The value of fc(t) can be determined using the following expression given in the Euro code 2

15(b).

Where ‘s’ is a coefficient that depends on the type of cement and equals 0.20 for high early strength cement (Class R), 0.25 for normal early strength cement (Class N), and 0.38 for slow early strength cement (Class S).

As the cement class will not be known at the design stage, Bamforth, et al., 2008 recommend assuming Class R and suggest that Class N can be assumed when the quantity of ground-granulated blast-furnace slag (GGBS) exceeds 35% or fly ash exceeds 20% in the cement. Similarly, when GGBS exceeds 65% or fly ash exceeds 35% in the cement, Class S may be assumed. It is important to note the strength gain of cement after 28 days is more dependent on the cement type than the cement strength class. Euro code 2 also warns that Eqn. (15) should not be used retrospectively to justify nonconforming reference strength.

Dynamic Modulus Of Elasticity

The dynamic modulus of elasticity of concrete, Ecd can be determined by the non-destructive electro-dynamic method, by measuring the natural frequency of the fundamental mode of longitudinal vibration of concrete prisms, as described in IS 516:1959. The dynamic modulus of elasticity has to be used in structures subjected to dynamic loading (i.e., impact or earthquake). The value of Ecd is generally 20%, 30%, and 40% higher than the secant modulus for high, medium- and low-strength concretes, respectively (Mehta and Monteiro 2006). More details about the dynamic modulus of elasticity may be found from Popovics, 2008.

Summary And Conclusions

The modulus of elasticity of concrete is required for the estimation of the deformation of buildings and members. The modulus of elasticity is dependent on the compressive strength of concrete, properties of the coarse aggregates, the proportion of the aggregates in the concrete, quality of cement paste, and addition of mineral admixtures. Accurate prediction of modulus of elasticity is important in reinforced and prestressed concrete structures while calculating member deformations, elastic shortening of columns, shrinkage and creep loss as well as crack width. Under normal conditions, the static modulus is specified, which is usually the secant modulus (slope of a line drawn from the origin to the point on the stress-strain curve corresponding to 40 % of the failure stress). The formulae specified in different codes are reviewed. It is seen that several codes consider only the strength of concrete to evaluate the elastic modulus, though a few consider the density of concrete, as well. A few researchers have recommended a formula that considers the effect of a wide range of aggregates and mineral admixtures. It is important for the Indian code, IS 456, to specify a formula, which considers the effect of as many factors as possible, in the evaluation of the elastic modulus of concrete, so that the deformations of structures are predicted accurately.

Acknowledgment

The author wishes to thank Dr. Ahmad Fayeq Ghowsi, Post-Doctoral Fellow at IIT, Delhi, for his help in making the drawings.

References

1. Interim bridge design specifications and commentary. American Association of Highway and Transportation Officials Washington (DC), 2006
2. ACI 318:2019 Building code requirements for Structural Concrete and Commentary, American Concrete Institute, Farmington Hills, 628.
3. ACI 363R-10 2010, State-of-the-art Report on High-strength Concrete, American Concrete Institute, Farmington Hills, 65.
4. AIJ Standard for Structural Calculations of Reinforced Concrete Structures, Chapter 2, Architectural Institute of Japan, Japan, 1985, 8-11.
5. Aïtcin P (2011) High performance concrete, CRC Press, Boca Raton, Fl.
6. AS-3600-18. Australian Concrete structures, Standards Australia, 2018, Australia, pp.45.
7. Bamforth, , Chisholm, D., Gibbs, J. and Harrison, T. (2008). Properties of Concrete for use in Eurocode 2, The Concrete Center Publication No. CCIP-029, U.K., 53 pp.
8. Bamforth, , Price, W.F., and Fleischer, C. C. (1997). “The late-life, insitu properties of Concrete in Nuclear Power Station Structures”, Nuclear Energy, Vol. 36, No.2, Apr., pp.149-160.
9. Comité Euro-International du Béton, “High-Performance Concrete, Recommended Extensions to the Model Code 90—Research Needs,” CEB Bulletin d’Information, 228, 1995, 46 pp.
10. Crouch, , Pitt, J. and Hewitt R. (2007) “Aggregate Effects on Pervious Portland Cement Concrete Static Modulus of Elasticity”, Journal of Materials in Civil Engineering, 2007, Vol. 19, No.7, pp. 561–568.
11. CSA A23.3-04 Design of Concrete Structures; Canadian Standards Association: Rexdale, ON, Canada,
12. ENV 1992-1-1, Eurocode Design of Concrete Structures—Part 1: General Rules and Rules for Buildings, 2004, 225 pp
13. IS 456:2000 Indian Standard Code of Practice for Plain and Reinforced Cement Concrete, 4th revision, Bureau of Indian Standards, New Delhi, 100.
14. IS 516:1959 (reaffirmed 2018), Method of Tests for Strength of Concrete, Bureau of Indian Standards, New
15. JSCE (2007). Guidelines for concrete 15, standard specifications for concrete structures- Design. Japan Society of Civil Engineering, Japan, 503 pp.
16. Jurowski, K., and Grzeszczyk, S. (2018) Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete, Materials, Vol.11, No.4, Apr., Doi: 10.3390/ma11040477
17. Mehta, K., and Monteiro, P. J. M. (2006) Concrete: Microstructure, Properties, and Materials, 3rd edition, McGraw-Hill, New York, p. 659.
18. Neville, M., Properties of Concrete, 4th Edition, 1996, John Wiley & Sons, New York, 844 pp.
19. Neville, M. and J.J. Brooks (2010) Concrete Technology, 2nd Edition, Pearson Education Canada, 464pp.
20. Noguchi, and Tomosawa, F. (1995). “Relationship between compressive strength and modulus of elasticity of high strength concrete.” Journal of Structural and Construction Engineering, (474), pp.1-10. (in Japanese)

21. Crouch, , Pitt, J. and Hewitt R. (2007) “Aggregate Effects on Pervious Portland Cement Concrete Static Modulus of Elasticity”, Journal of Materials in Civil Engineering, 2007, Vol. 19, No.7, pp. 561–568.
22. CSA A23.3-04 Design of Concrete Structures; Canadian Standards Association: Rexdale, ON, Canada,
23. ENV 1992-1-1, Eurocode Design of Concrete Structures—Part 1: General Rules and Rules for Buildings, 2004, 225 pp
24. IS 456:2000 Indian Standard Code of Practice for Plain and Reinforced Cement Concrete, 4th revision, Bureau of Indian Standards, New Delhi, 100.
25. IS 516:1959 (reaffirmed 2018), Method of Tests for Strength of Concrete, Bureau of Indian Standards, New
26. JSCE (2007). Guidelines for concrete 15, standard specifications for concrete structures- Design. Japan Society of Civil Engineering, Japan, 503 pp.
27. Jurowski, K., and Grzeszczyk, S. (2018) Influence of Selected Factors on the Relationship between the Dynamic Elastic Modulus and Compressive Strength of Concrete, Materials, Vol.11, No.4, Apr., Doi: 10.3390/ma11040477
28. Mehta, K., and Monteiro, P. J. M. (2006) Concrete: Microstructure, Properties, and Materials, 3rd edition, McGraw-Hill, New York, p. 659.
29. Neville, M., Properties of Concrete, 4th Edition, 1996, John Wiley & Sons, New York, 844 pp.
30. Neville, M. and J.J. Brooks (2010) Concrete Technology, 2nd Edition, Pearson Education Canada, 464pp.
31. Noguchi, and Tomosawa, F. (1995). “Relationship between compressive strength and modulus of elasticity of high strength concrete.” Journal of Structural and Construction Engineering, (474), pp.1-10. (in Japanese)
32. Noguchi, , Tomosawa, F., Nemati, K.M., Chiaia, B.M., and Fantilli, A.P. (2009) “A Practical Equation for Elastic Modulus of Concrete”, ACI Structural Journal, Vol.106, No.5, pp. 690-696.
33. NZS 3101- Part 1:2006, The Design of Concrete Structures, Part 2: Commentary, Standards, Wellington, New
34. Popovics, (2008). A Study of Static and Dynamic Modulus of Elasticity of Concrete, Final Report, American Concrete Institute – Concrete Research Council, Urbana, IL., 16 pp.
35. Singh, P. Yazdani, N., and Ramirez (2013) “Effect of Time-dependent Concrete Modulus of Elasticity on Prestress Losses in Bridge Girders”, International Journal of Concrete Structures and Materials, Vol. 7, pp. 183-191.
36. SP-52-101-2003. Concrete and Reinforced Concrete Structures Without Prestressing, Gosstroi, Russia, Moscow, 2004, 55
37. Subramanian, N. (2019). Building Materials, Testing, and Sustainability, Oxford University Press, New Delhi, 788
38. Swamy, N. (1985) “High-Strength Concrete-Material Properties and Behavior”, ACI SP87-8, pp. 119–145
39. Topcu, B., and Ugurlu, A. (2007), “Elasticity Theory of Concrete and Prediction of Static E-modulus for Dam Concrete using Composite Models”, Teknik Dergi, Vol.18, No.1, pp. 4055-4067.
40. Vakhshouri, , and Nejadi, S. (2019) “Empirical Models and Design Codes in Prediction of Modulus of Elasticity of Concrete”, Frontiers of Structural and Civil Engineering, Vol. 13, pp. 38–48.
41. Zhang, H and Gjvorv, O. E. (1991) “Mechanical Properties of High-Strength Lightweight Concrete”, Materials Journal, Vol. 88, No.3, pp. 240–247.